Ondas Estacionárias em um Corda Vibrante

outubro 23, 2017

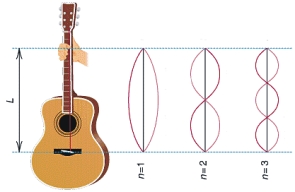Fonte:http://www.fisicapaidegua.com/teoria/acustica/violao_02.jpg

Em uma corda onde duas ondas senoidais com a mesma amplitude e o mesmo comprimento de onda se propagam em sentidos opostos, a interferência mútua produz uma onda estacionária

Uma onda estacionária é caracterizada por ter uma forma que não se move, ou seja, ela tem uma forma estática, pois devido a interferência os pontos de máximo e mínimo não variam no tempo. Outra característica desse tipo de onda é a existência de pontos chamado de nós, os quais ficam constantemente imóveis, enquanto isso o ponto médio entre dois nós é chamado de antinós, onde a onda tem amplitude é máxima.

A equação de descrever uma onda estacionária é dada por:

Equação 1

Sendo que essa equação é obtida somando a equação de duas ondas iguais que se propagam numa corda em sentidos contrários, assim as grandezas a seguir são iguais para as essas duas ondas: amplitude máxima Ym, frequência angular ω, número de onda k, período T, e velocidade v.

As relações entres essas grandezas são descritas pelas seguintes equações:
Equação 2

Equação 3

Equação 4

Equação 5

Com τ sendo a tensão aplicada na corda com densidade linear μ.

Diferente de um onda senoidal progressiva, em um onda estacionária a amplitude varia com a posição. Na onda da equação 1, a amplitude é zero para valores de kx tais que sen(kx) = 0. Esses valores são dados pela relação:

Equação 6

com n=0,1,2,3,4,....

Utilizando a equação 3:

Equação 7

com n=0,1,2,3,4,.... Sendo o número de nós.Quando uma onda estacionária é gerada existe uma ressonância em que a corda ressoa numa dada frequência, essas frequências em que a corda ressoa são conhecidas como frequências de ressonância, se a corda for posta para oscila numa frequência que não seja uma frequência de ressonância a corda não formará uma onda estacionária.
Em uma corda de comprimento L que possui extremidades fixas, terá as frequências de ressonância calculadas por:

Equação 8

com n=0,1,2,3,4,....

Quando n=1, é obtida menor frequência de oscilação a qual é chamada de modo fundamental ou primeiro harmónico, quando n=2 o modo de oscilação e chamado de segundo harmónico, e assim por diante.

Para compreende melhor o assunto é possível realizar um simples experimento para criar ondas estacionarias, para isso é preciso de um motor elétrico, uma pilha, um barbante, fita adesiva, e um pequeno objeto para ser utilizado como peso.

Para monta o experimento é preciso prende com a fita adesiva, uma ponta do barbante no peso e a outra no eixo do moto, depois é só liga o motor na pilha. Quando o motor começar a gira, será observado a formação de ondas estacionaria, caso isso não aconteça, será preciso troca o peso por um mais leve, ou mais pesado. Como sugestão tende varia o comprimento do barbante ou o número de pilhas a ser utilizado, e observe como isso influencia nas ondas. Pode-se observar um exemplo do experimento a seguir.